PTfS25: Assignment 10: OpenMP scaling, 3D stencil

Opened: Monday, 7 July 2025, 10:05 AM

Due: Thursday, 17 July 2025, 10:05 AM

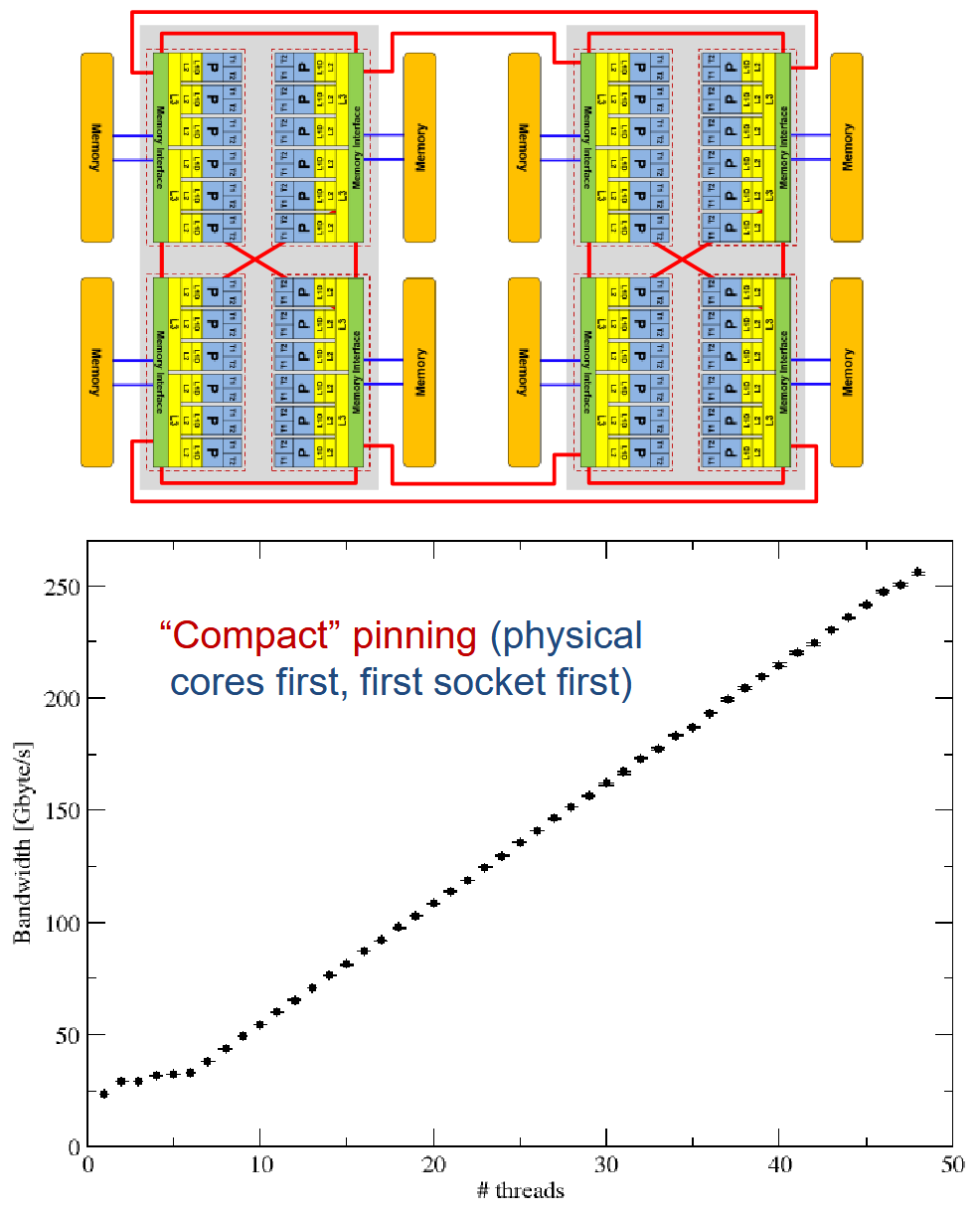
Scaling behavior. In the lecture (slide set 10, slide 30) we showed you a graph of memory bandwidth vs. number of cores for the STREAM Triad benchmark on a 48-core AMD EPYC (Zen) node:

This data was taken with a simple OpenMP-parallel loop:
```
      #pragma omp parallel for schedule(static)
      for(int i=0; i<N; ++i)
        a[i] = b[i] + s * c[i];
    
```
The working set was constant (5 GB). Compact pinning was employed, i.e., the cores of the machine were filled consecutively from left to right.

(a) (5 crd) Look at the structure of the compute node above. How many ccNUMA domains does it have?
(b) (5 crd) From the data in the graph, estimate the maximum memory bandwidth of one ccNUMA domain. You may assume that nontemporal stores or cache line claim are not available.
(c) (15 crd) Why does the code scale linearly beyond the first ccNUMA domain while showing saturating behavior on the first domain?
(d) (5 crd) Describe what the scaling would look like if we chose to "scatter" the threads evenly throughout the machine (always choosing a number of threads that is a multiple of the number of ccNUMA domains).
Triangular parallel MVM. Consider the multiplication of a dense lower triangular matrix with a vector in double precision (we store the full matrix but just use the lower triangular part of it):
```
for(r=0; r<N; ++r)
  for(c=0; c<=r; ++c) 
    y[r] += a[r][c] * x[c];
```
(a) (15 crd) Write a benchmark code for this operation, along the lines of what we did with the simple streaming loops. Parallelize it with OpenMP and run it with 1...18 threads on one ccNUMA domain of a Fritz socket at a problem size (NxN) of 12000x12000. Do not forget to initialize all data structures with sensible data.
(b) (10 crd) Which loop should be parallelized? What is the optimal OpenMP loop schedule? Why?
(c) (15 crd) Plot performance vs. number of cores for the default loop schedule and the best loop schedule you could identify.
(d) (10 crd) Run the code on the four ccNUMA domains of a full node (72 cores). is the loop schedule you chose above now still optimal? Can you modify the code or otherwise change how you run it in order to improve the scaling? Describe your steps in detail.
Performance modeling of a 3D Jacobi smoother. Consider the following OpenMP-parallel 3D Jacobi code:
```
#pragma omp parallel private(iter)
{
  for(iter=0; iter<maxiter; ++iter) {
    #pragma omp for schedule(static)
    for(k=1; k<N-1; ++k) {
      for(j=1; j<N-1; ++j) {
        for(i=1; i<N-1; ++i) {
          f[t1][k][j][i] = 1./6. * 
                      (f[t0][k-1][j][i]+
                       f[t0][k+1][j][i]+
                       f[t0][k][j-1][i]+
                       f[t0][k][j+1][i]+
                       f[t0][k][j][i-1]+
                       f[t0][k][j][i+1]);
        }
      }
    }
    swap(t0,t1);
  }
}
```
Assume that N=350, all arrays are in double precision, and that we run this code on all cores of a ten-core Intel "Ivy Bridge" processor (25 MiB of shared L3 cache, 256 KiB of per-core L2 cache, 32 KiB of per-core L1, memory bandwidth of 41 GB/s, clock frequency 2.0 GHz).

(a) (5 crd) Is the code correct? If it is not, fix it.

(b) (10 crd) Someone says: "It is better to choose the data layout f[k][j][i][t], because the source and the target arrays are handled together in the same loop, and it will be better to interleave them." What is your comment on this?

(c) (15 crd) What happens if we use schedule(static,1) at N=350? Assume the original data layout. What is the expected performance in this case compared to the default (static) schedule?