Exercise: π by the Monte Carlo method

Here we want to use OpenMP and MPI to calculate π using a very simple (and inefficient) method.

------

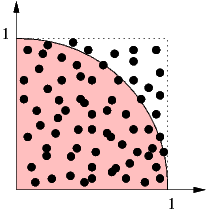
The quarter circle in the first quadrant with origin at (0,0) and radius 1 has an area of π/4. Look at the random number pairs in [0, 1] × [0, 1]. The probability that such a point lies inside the quarter circle is π/4, so given enough statistics we are able to calculate π using this “Monte Carlo” method.

1. You can find a serial version (C and Fortran90) in the folder MCPI. If you just type "make", it will build the C and Fortran versions automatically. The program prints its runtime and the relative accuracy of the computed approximation to π. 
   
   
2. Parallelize the code using OpenMP. Note the use of the rand_r() function to get separate random number sequences for all threads. What is the relative accuracy that you can achieve with all 112 cores of a node? 
   
   In order to compile an OpenMP program, you have to use the -qopenmp option on the Intel compiler command line. Also do not forget to start a batch job and run the code on a compute node, else you will share resources with many other users on the frontend.
   
   
3. Why did we use rand_r() at all instead of plain rand()? Try it and see what happens!
   
   --------- Continue below afer the "MPI in depth" lecture ----------
   
   
4. Parallelize the program with MPI. To get started you can use the "Hello World" MPI program example from earlier and take it from there using the lecture slides.
   
   Reminder: In order to compile an MPI program, you have to use one of the wrapper scripts mpiicx, mpiicpx, or mpiifx instead of the normal Intel compiler for C, C++, and Fortran code, respectively. For running the code you use mpiexec in your batch script:
   
   $ mpiexec -n # ./my_executable
   
   Here, "#" is the number of processes you want to use. Each CoolMUC-4 node has 112 cores, so if you allocate one node you can run up to 112 processes. (Note: mpirun -np # ./my_executable will also work)