Assignment 3

f(x) = 4/(1+x²)

int SLICES = 2000000000;
double delta_x = 1./SLICES;
for (int i=0; i < SLICES; i++) {
  x = (i+0.5)*delta_x;
  sum += (4.0 / (1.0 + x * x));
}
Pi = sum * delta_x;

---

(a) Convert this code fragment into a working program.
(b) Parallelize it with OpenMP and make sure, of course, that the result is still π (well, sort of).
(c) Add a time measurement and report performance in iterations per second. How much faster is your code with 20 threads (the maximum number of cores on an Emmy node) than with a single thread? Hence, what is the parallel efficiency at 20 threads?
(d) Is there any relevant statistical variation in the runtime between runs? If so, report the minimum, the maximum, and the median across 20 runs.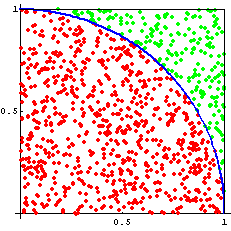

π by the Monte Carlo method. The quarter circle in the first quadrant with origin at (0,0) and radius 1 has an area of π/4. Look at the random number pairs in [0, 1] × [0, 1]. The probability that such a point lies inside the quarter circle is π/4, so given enough statistics we are able to calculate π using this so-called “Monte Carlo” method.
(a) Write a parallel OpenMP program that performs this task. Use the rand_r() function to get separate random number sequences for all threads. Make sure that adding more threads does not harm the statistics (how is this achieved?).
(b) What is the best relative accuracy that you can achieve with twenty "Emmy" cores in one second of walltime? Consider and describe any code optimizations (beyond parallelization) that can speed up the computation!
(Hint: You may assume that the random number function rand_r() produces "perfect" random numbers with no correlations whatsoever)