1. π by the Monte Carlo method
Completion requirements
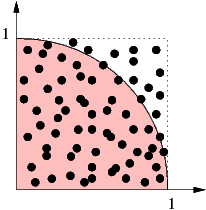 The quarter circle in the first
quadrant with origin at (0,0) and radius 1 has an
area of π/4. Look at the random number pairs in [0, 1] × [0, 1]. The
probability that such a point lies inside the quarter circle is π/4, so
given enough statistics we are able to calculate π using this “Monte
Carlo” method.
The quarter circle in the first
quadrant with origin at (0,0) and radius 1 has an
area of π/4. Look at the random number pairs in [0, 1] × [0, 1]. The
probability that such a point lies inside the quarter circle is π/4, so
given enough statistics we are able to calculate π using this “Monte
Carlo” method.
- You can find a serial version (C and Fortran90) in the pi-monte-carlo directory. When compiled, the program prints its runtime and the relative accuracy of the computed approximation to π.
- Parallelize the code using OpenMP.
- ensure the relevant variables are made shared or (first)private
- use the corresponding reduction clause for aggregation of variables
Note the use of the rand_r() function to get separate random number sequences for all threads.
What is the best relative accuracy that you can achieve with all cores?
In order to compile an OpenMP program, you have to use the -fopenmp (gcc/clang/gfortran) or the -qopenmp (icc/ifort/...) option.
For the C version you might also need to link against the math library by adding -lm.
OpenMP runtime functions you might need:- omp_get_thread_num(): returns the thread id of a thread, in the range of 0 to no. of threads - 1
- omp_get_max_threads(): returns no. of threads used in the next parallel region
- omp_get_wtime(): returns no. of seconds since some point in time
Why did we use rand_r() at all instead of plain rand()? Try it and see what happens!
Last modified: Monday, 20 March 2023, 4:39 PM
