Exercise: MCPI-PtP

Here we want to use MPI to speed up the calculation of π using the Monte Carlo method. It is a simple (and inefficient) method to calculate π but it is easy for MPI parallelization.  The workload distribution and one line after MPI calls contain missing parts labeled with FIXME markers each of which needs to be replaced by the correct piece of code.

------

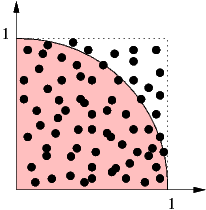
The quarter circle in the first quadrant with origin at (0,0) and radius 1 has an area of π/4. We look at the random number pairs in [0, 1] × [0, 1]. The probability that such a point lies inside the quarter circle is π/4, so given enough statistics we are able to calculate π using this “Monte Carlo” method.

1. You can find incomplete codes both in C and Fortran in the folder MCPI-PtP. After correcting the FIXME markers, if you just type "make", it will build the C or Fortran code automatically and create an executable called mcpi-ptp. When running the program, it will print its runtime and the relative accuracy of the computed approximation to π. 
   
   
2. Note that we want to use the rand_r() function so that we get distinct random number sequences for all MPI processes. If you have the same set of random numbers for all processes, then for a fixed total number of points, using more processes will reduced the accuracy. One of FIXME markers is related to this point. By making the seed of the random number generator being independent on the rank of the process, you can check the loss of accuracy.
   
   
3.  What is the best relative accuracy that you can achieve with all 72 cores of a node in one second of walltime?