Assignment 8
- MPI-parallel raytracer. Parallelize the raytracer from an earlier assignment with MPI. This can be done with simple MPI calls, using the calc_tile() function as the basic unit of work.
(a) Use an overall problem size of 8000x8000 pixels and report performance in MPixels/s on 1...40 physical cores (up to 2 nodes) of Emmy (i.e., strong scaling). What is the optimal tile size here? Why can tiles not be as small as in the OpenMP code?
(b) Add code to calculate the average gray value across all pixels using an MPI collective operation. What is the average gray value?
Hint: The easiest approach to MPI parallelization is a "master-worker" scheme where one process (the master) sends out work and receives finished tiles from the workers. There may be other solutions, though. - Dense matrix-vector multiplication. Complete the code snippet presented in the lecture for MPI-parallel dense MVM to get a running program.
(a) Perform strong scaling runs on 1...80 processes (up to four Emmy nodes) using the plain blocking point-to-point communication strategy as explained in the lecture. Use problem (matrix) sizes of 1000x1000, 4000x4000, and 10000x10000.
(b) Is there a way to overlap the ring shift communication of the RHS vector with useful work? Rewrite the code using nonblocking MPI point-to-point calls, assuming that these provide fully asynchronous communication. Dou you see a performance difference to the original version?
(c) Using your ping-pong microbenchmark measurements, can you estimate a memory-bound problem size below which the communication overhead would be significant?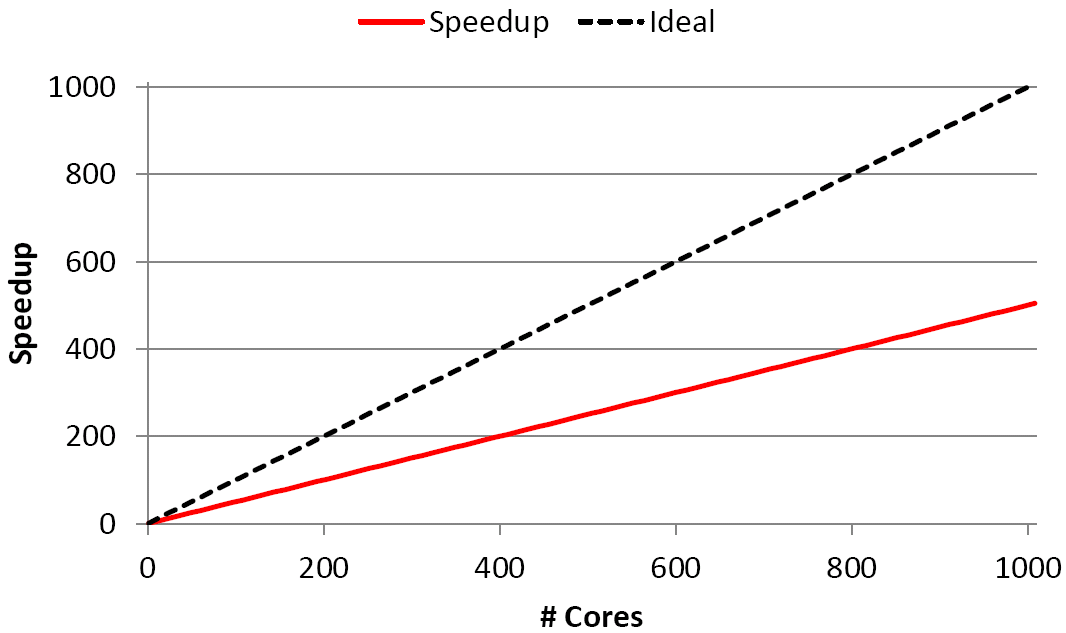 
Speedup games. A speaker at a conference presents performance data for her highly scalable code on up to 1000 cores of a recent multicore-based supercomputer platform (see the graph on the right). She says "We achieve a parallel efficiency of about 0.5 on 1,000 cores, so there must be hidden optimization potential that we will investigate."
What is the natural question to ask?
Last modified: Thursday, 10 December 2020, 2:49 PM